函数作为入门知识,在各地的中考考试试题中主要以填空题、选择题的形式来考查函数的基本定义、函数自变量的取值范围、函数之间的变化规律及其图象。
考试大纲需要:
1、会画平面直角坐标系,并能依据点的坐标描出点的地方,由点的地方写出点的坐标。
2、学会坐标平面内点的坐标特点。
3、知道函数的有关定义和函数的表示办法,并能结合图象对实质问题中的函数关系进行剖析.
4、能确定函数自变量的取值范围,并会求函数值。
01
平面直角坐标系与点的坐标特点
1.平面直角坐标系
如图,在平面内,两条互相垂直的数轴的交点O称为原点,水平的数轴叫__________,竖直的数轴叫__________,整个坐标平面被x轴、y轴分割成四个象限.



02
距离与点的坐标的关系
1.点与原点、点与坐标轴的距离
点P到x轴和y轴的距离分别是|y|和|x|,点P到坐标原点的距离为

03
函数有关的定义及图像

04
函数自变量取值范围的确定
确定自变量取值范围的办法:

考试知识点1、平面直角坐标系内点的坐标特点

办法总结:解这种题的重点是明确各象限内点的坐标特点,总结规律,再结合规律列出不等式求解
考试知识点2、图形的变换与坐标


办法总结 :在平面直角坐标系中,图形的平移、对称、旋转等变换会引起坐标的变化,同样,坐标的变化也会引起图形的变换,两者紧密结合充分体现了数形结合的思想.
考试知识点3、函数的定义
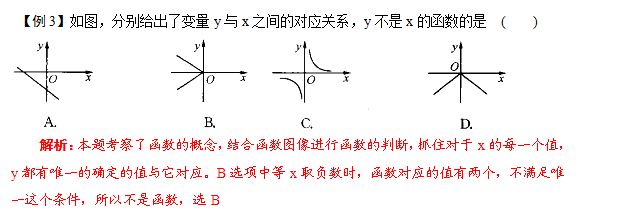
办法总结 :在平面直角坐标系中,图形的平移、对称、旋转等变换会引起坐标的变化,同样,坐标的变化也会引起图形的变换,两者紧密结合充分体现了数形结合的思想.
考试知识点4、函数图像的应用

办法总结 :借助函数关系和图像剖析解决实质问题,要透过问题情境准确地探寻出问题的自变量和函数,要看清横坐标和纵坐标表示的是哪两个变量,探求变量和函数之间的变化趋势,注意观察图像的“走势”特征,合理地剖析变化过程,准确地结合图像解决实质问题.
考试知识点5、函数自变量取值范围的确定

办法总结 :自变量的取值需要使含自变量的代数式有意义
主要体目前以下几种:
含自变量的分析式是整式:自变量的取值范围是全体实数;
含自变量的分析式是分式:自变量的取值范围是使得分母不为0的实数;
含自变量的分析式是二次根式:自变量的取值范围是使被开方法为非负的实数;
含自变量的分析式既是分式又是二次根式时:自变量的取值范围是它们的公共解,一般列不等式组求解;
当函数分析式表示实质问题时:自变量的取值需要使实质问题有意义.







